Word2vecまとめ
Word2vecは「周辺にある単語が似ている単語同士は意味も似ている」というハリスの分布仮説に基づき,ある単語から周辺単語を予測するSkip-gram(SG)モデルと周辺単語からある単語を予測するContinuous Bag of Words(CBOW)モデルの2種類あります.ネットワークの構造は入力層->中間層->出力層の(入力層は数えないから)2層のニューラルネットワークからなります.word2vecに関してはわかりやすい記事があるが自分の頭の中の整理のためblogにまとめるることにしました.ちなみにわかりやすい記事というのは
概要を掴むだけなら
word2vec(Skip-Gram Model)の仕組みを恐らく日本一簡潔にまとめてみたつもり - これで無理なら諦めて!世界一やさしいデータ分析教室数式も含めて詳しく知りたいなら
Word2Vec のニューラルネットワーク学習過程を理解する · けんごのお屋敷
以下に自分のまとめを書いていきます.
理論的な話
上記に書いたとおりword2vecはハリスの分布仮説に基づいて注目単語があったときに周辺単語がある確率(条件付き確率)を最大化するといったことをしてベクトルを作っています.具体的な数式は以下のようになっています.
\begin{align}
P(C_t|w_t) &= \prod_{c_i \in C_t} p(c_i|w_t) \label{eq:based_equation} \\
&= p(c_1 \land c_2 \cdots \land c_n | w_t) \nonumber \\
&= p(c_1|w_t) \times p(c_2|w_t) \times \cdots \times p(c_n|w_t) \nonumber \\
\end{align}
実際は単語の共起関係に独立性は成り立たないので上記の式のようにならないのですが計算の簡略化のために一般に独立であると仮定されて計算しています.
どうモデル化するか
前処理
Word2vecモデルを学習させるためには単語をone-hotベクトルというベクトルにする必要があります.このone-hotベクトルをモデルの入力にします.
例えば下記のように,
Skip-gramモデル
Skip-gramモデルは1つの単語に対して周辺の単語を予測するモデルで最大化すべき目的関数(損失関数)は以下の式\eqref{eq:maximize_func}です.式\eqref{eq:based_equation} \begin{align} \sum_{t=1}^{T} \sum_{-c \le j \le c, j\neq 0} \log p(w_{t+j}|w_t) \label{eq:maximize_func} \end{align} また式\eqref{eq:maximize_func}内の条件付き確率は式\eqref{eq:conditional_probability}で表されます. \begin{align} p(w_{t+j}|w_t)=\frac{\exp \left(v_t^{\mathrm{T}}\; v_{t+j}\right)}{\sum_{k=1}^{|V|}\exp \left(v_t^{\mathrm{T}}\; v_k\right)} \label{eq:conditional_probability} \end{align}
変数について
式\eqref{eq:maximize_func},式\eqref{eq:conditional_probability}中の変数について,$c$はwindowサイズ.注目する単語から$2\times c$個の周辺単語を学習の際に用います.$w_t$は注目している単語,$w_{t+j}$は$w_t$の周辺単語.つまり,注目している単語$w_t$の前後$c$個ずつ,合計$2\times c$個の単語が周辺単語$w_{t+j}$となります.$v_t$は単語$w_t$を表す特徴ベクトル.$v_{t+j}$は周辺単語$w_{t+j}$を表す特徴ベクトル.$V$は全単語の集合.$|V|$はすべての単語数,$T$は文書中の単語の総数(重複含む)を表します.この変数の中の単語の特徴ベクトルを学習で求めます.また,この特徴ベクトルのことを「分散表現」や「埋め込みベクトル(Embedding vector)」といったりします.式の意味
上記の式\eqref{eq:maximize_func}は文章中に単語$w_t$があったとき単語$w_{t+j}$($w_t$の前後の単語)が出現する確率を表しています.つまり,文章中に並んで出現しているので「$w_t$が出現したときに$w_{t+j}$が出現する確率」(条件付き確率)を大きくしたいというのが目的です.式\eqref{eq:conditional_probability}の分母は全単語のベクトル$v_k$と注目単語のベクトル$v_t$の内積をeの肩に乗せたもの.分子は周辺単語のベクトル$v_{t+j}$と注目単語のベクトル$v_t$の内積をeの肩に乗せたもの.これは注目単語が出現したときに共起した単語の単語ベクトル(周辺単語ベクトル)が出現する確率(条件付き確率)を表しています.式\eqref{eq:maximize_func}を最大化するというのは共起している単語のベクトル同士の内積の値を高くするということです.
この計算は大変なので階層的softmaxやNegative samplingによって学習する際の計算コストを削減する.
なぜ現実的でないかというと,単語の種類が例えば10,000単語だとする($|V| = 10,000$).
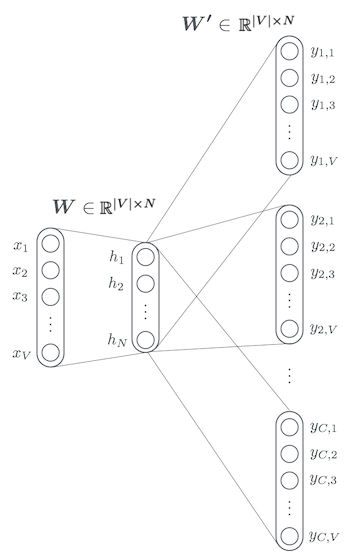
Skip-gram model.
順伝播の計算
具体的な順伝播の計算を以下に書く.1単語から1単語を予測する図のようなCBOWのモデルを簡単のため考える.
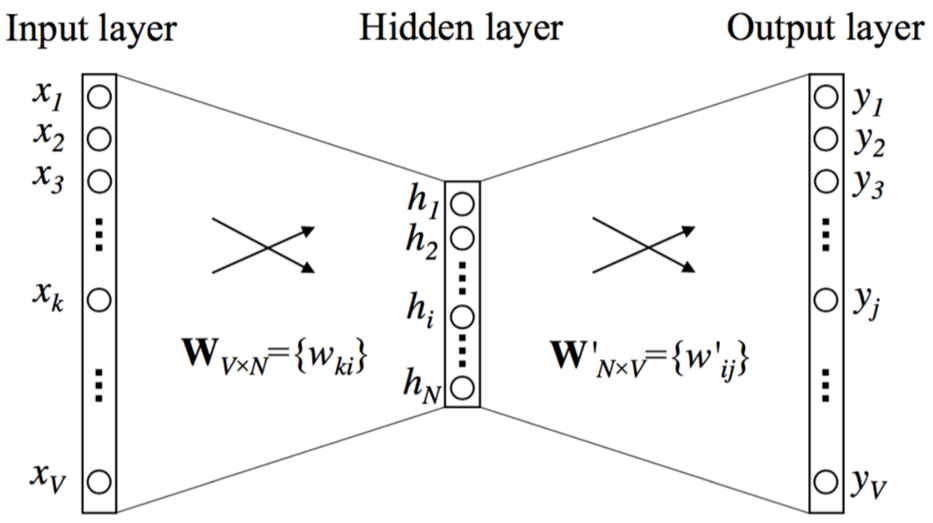
Simple Skip-gram model.
変数について説明する.$|V|$は全単語の数,$c$はwindowサイズ,$N$は中間層の次元.入力ベクトル$\boldsymbol{x}={x_1, x_2, \cdots, x_{|V|}}$はone-hotベクトル.one-hotベクトルとはある1つの$x_k$に対して1の値を取り,それ以外の$x_{k’}$では0を取るようなベクトルである($x_k=1, x_{k’}=0 \;\; \rm{for} \;\; k\neq k’$). 入力層と中間層の間の重み行列は$|V|\times N$行列である.それぞれの行は$N$次元のベクトル$\boldsymbol{v}_{w}$であり,$\boldsymbol{v}_{w}$は入力層の単語$w$に対応したベクトルである.
Negative Sampling
共起する単語と共起しない単語の変数について考える必要あり.
$w_c$とか$w_r$とか...
skip-gramモデルをベースとした学習の計算をより効率的に行う手法である.基本的な考え方は注目している単語と単語の集合からランダムにとってきた単語のうち,windowサイズの範囲内にある単語(注目している単語とよく共起する単語)については確率が高く,それ以外の単語については共起しない確率が高くなるような目的関数を設定しその関数を最大化するように学習する.
注目する単語$w_t$が単語$w_c$と共起している確率(windowサイズ内に出現する確率)を$p(w_c|w_t)$と表すと,$w_c$が共起しない確率は$1-p(w_c|w_t)$と表せる.$p(w_c|w_t)$をsigmoid関数で表すと$p(w_c|w_t)$は以下のように表せる. \begin{align} p(w_c|w_t) = \sigma(v_t^{\mathrm{T}} \; v_c) = \frac{1}{1+\exp (-v_t^{\mathrm{T}} \; v_c)} \nonumber \end{align}
よって$w_c$が共起しない確率$1-p(w_c|w_t)$は以下のようになる.
\begin{align}
1-p(w_c|w_t) = 1-\sigma(v_t^{\mathrm{T}} \; v_c) &= 1-\frac{1}{1+\exp (-v_t^{\mathrm{T}} \; v_c)} \nonumber \\
&=\frac{1 + \exp (-v_t^{\mathrm{T}} \; v_c) -1}{1+\exp (-v_t^{\mathrm{T}} \; v_c)} \nonumber \\
&=\frac{\exp (-v_t^{\mathrm{T}} \; v_c)}{1+\exp (-v_t^{\mathrm{T}} \; v_c)} \nonumber \\
&=\frac{1}{\exp (v_t^{\mathrm{T}} \; v_c)+1} \nonumber \\
&=\frac{1}{1+\exp (v_t^{\mathrm{T}} \; v_c)} \nonumber \\
&\Bigl( =\sigma(-v_t^{\mathrm{T}} \; v_c) \Bigr) \nonumber
\end{align}
これらを用い,新たに以下の式\eqref{eq:new_maximize_func}を目的関数に設定する.
\begin{align}
&-\log p(w_c|w_t)\prod_{w_r \, \in V_{neg}}(1-p(w_r|w_t)) \nonumber\\
\Leftrightarrow &-\log \sigma(v_t^{\mathrm{T}} \; v_c)\prod_{w_r \, \in V_{neg}}(1-\sigma(v_t^{\mathrm{T}} \; v_r)) \nonumber\\
\Leftrightarrow &-\left(\log \sigma(v_t^{\mathrm{T}} \; v_c) + \log \prod_{w_r \, \in V_{neg}}(1-\sigma(v_t^{\mathrm{T}} \; v_r)) \right) \nonumber\\
\Leftrightarrow &-\left(\log \sigma(v_t^{\mathrm{T}} \; v_c) + \sum_{w_r \, \in V_{neg}}\log (1-\sigma(v_t^{\mathrm{T}} \; v_r)) \right) \nonumber\\
\Leftrightarrow &-\left(\log \sigma(v_t^{\mathrm{T}} \; v_c) + \sum_{w_r \, \in V_{neg}}\log \sigma(-v_t^{\mathrm{T}} \; v_r) \right) \nonumber\\
\Leftrightarrow &-\log \sigma(v_t^{\mathrm{T}} \; v_c) - \sum_{w_r \, \in V_{neg}}\log \sigma(-v_t^{\mathrm{T}} \; v_r)
\label{eq:new_maximize_func}
\end{align}
$V_{neg}$は注目する単語と共起しない単語の集合.つまりwindowサイズの外から選ばれた単語.この目的関数を最大化するということは,注目する単語$w_t$と共起する単語$w_c$についての確率は大きくし,注目する単語と共起しない単語$w_r$に対しての確率は小さくするような操作である.
memo
word2vecはある単語のベクトルをよく共起している単語同士で近似している(Autoencoderと同じネットワーク構造のため).そのため,よくある例のking - man + woman = queenではkingとmanに共通するベクトル情報が落ち,その後womanのベクトル情報が加わるので結果的にqueenが出てきていると考えられる.
ネットワーク構造はAutoencoderと同じだが目的関数(損失関数)が異なるので...
\begin{align}
\boldsymbol{v}_{man} &= \boldsymbol{a}_1 \nonumber \\
\boldsymbol{v}_{woman} &= \boldsymbol{a}_2 \nonumber \\
\boldsymbol{v}_{king} &= \boldsymbol{a}_1 + \boldsymbol{a}_3 + \boldsymbol{a}_4 \nonumber \\
\boldsymbol{v}_{queen} &= \boldsymbol{a}_2 + \boldsymbol{a}_3 + \boldsymbol{a}_4 \nonumber
\end{align}
例えば,word2vecで上のような学習がされているとするとking - man + woman = queenというのが求められるのがわかる.(実際はこんな簡単なベクトルで表されていないはず...)
References
- Distributed Representations of Words and Phrases and their Compositionality
- Yoav Goldberg and Omer Levy, word2vec Explained: deriving Mikolov et al.’s negative-sampling word-embedding method
- The backpropagation algorithm for Word2Vec | Marginalia
- A Word2Vec Keras tutorial - Adventures in Machine Learning
- David Meyer, How exactly does word2vec work?
- word2vec(Skip-Gram Model)の仕組みを恐らく日本一簡潔にまとめてみたつもり - これで無理なら諦めて!世界一やさしいデータ分析教室
- Word2Vec のニューラルネットワーク学習過程を理解する · けんごのお屋敷
- word2vecのソースを読んでみた